Sec 3 3 Right Triangle Trigonometry Form

What is the sec 3 3 right triangle trigonometry

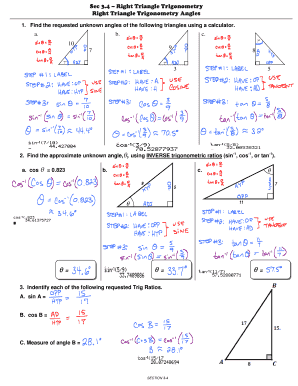
The sec in trigonometry, specifically within the context of a right triangle, refers to the secant function. In a right triangle, the secant of an angle is defined as the ratio of the length of the hypotenuse to the length of the adjacent side. For example, if you have a right triangle where one angle measures three degrees, the secant of that angle can be calculated using the formula: sec(θ) = hypotenuse / adjacent. This function is particularly useful in various applications, including physics and engineering, where understanding the relationships between angles and side lengths is crucial.

How to use the sec 3 3 right triangle trigonometry

To effectively use the sec in trigonometry for a right triangle, begin by identifying the angles and the lengths of the sides. For a right triangle, label the sides as follows: the hypotenuse (the longest side), the opposite side (the side opposite the angle of interest), and the adjacent side (the side next to the angle of interest). Once these sides are identified, apply the secant function by using the formula sec(θ) = hypotenuse / adjacent. For instance, if the hypotenuse measures five units and the adjacent side measures four units, the secant of the angle would be calculated as sec(θ) = 5 / 4 = 1.25.

Examples of using the sec 3 3 right triangle trigonometry

Consider a right triangle where the hypotenuse is six units and the adjacent side is four units. To find the secant of the angle adjacent to the side of four units, you would calculate sec(θ) = 6 / 4 = 1.5. Another example could involve a right triangle with a hypotenuse of ten units and an adjacent side of eight units. Here, sec(θ) would equal 10 / 8 = 1.25. These examples illustrate the practical application of the sec function in determining relationships between angles and side lengths in right triangles.

Steps to complete the sec 3 3 right triangle trigonometry

To complete calculations involving the sec in trigonometry for a right triangle, follow these steps:

1. Identify the right triangle and label the sides: hypotenuse, opposite, and adjacent.
2. Measure the lengths of the hypotenuse and the adjacent side accurately.
3. Use the secant formula: sec(θ) = hypotenuse / adjacent.
4. Perform the division to find the secant value.
5. Interpret the result in the context of your specific application, whether it be in physics, engineering, or another field.

Legal use of the sec 3 3 right triangle trigonometry

Understanding the sec in trigonometry can have legal implications, especially in fields such as architecture and engineering, where accurate measurements are critical. For instance, when designing structures, professionals must ensure that angles and lengths adhere to safety regulations and building codes. Miscalculations can lead to structural failures, resulting in legal consequences. Therefore, using the secant function correctly helps ensure compliance with legal standards in construction and design.

Key elements of the sec 3 3 right triangle trigonometry

Key elements to consider when working with the sec in trigonometry include:

• The definition of secant as a ratio of the hypotenuse to the adjacent side.
• The relationship between angles and side lengths in right triangles.
• The importance of accurate measurements for practical applications.
• Understanding how secant relates to other trigonometric functions, such as sine and cosine.