We are not affiliated with any brand or entity on this form.

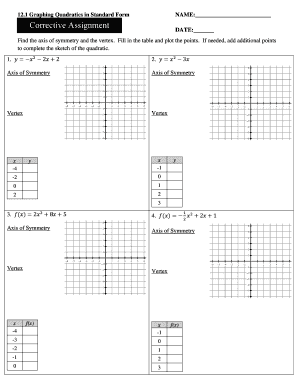
12 1 Graphing Quadratics in Standard Form

Use a 12 1 graphing quadratics in standard form template to make your document workflow more streamlined.

How it works

Open form follow the instructions

Easily sign the form with your finger

Send filled & signed form or save

What is the 12 1 Graphing Quadratics In Standard Form

The 12 1 graphing quadratics in standard form is a mathematical representation used to describe quadratic equations. In this format, the equation is expressed as y = ax² + bx + c, where a, b, and c are constants. This standard form is essential for graphing parabolas, allowing for easy identification of key features such as the vertex, axis of symmetry, and direction of opening. Understanding this form is crucial for students and professionals working with quadratic functions in various fields, including engineering and economics.

How to use the 12 1 Graphing Quadratics In Standard Form

Using the 12 1 graphing quadratics in standard form involves several steps. First, identify the coefficients a, b, and c from the equation. Next, calculate the vertex using the formula x = -b/(2a) to find the x-coordinate, and substitute this value back into the equation to find the corresponding y-coordinate. This gives you the vertex point. From there, you can determine the axis of symmetry, which is the vertical line through the vertex. Finally, plot additional points by selecting values for x and calculating y to create a complete graph of the quadratic function.

Steps to complete the 12 1 Graphing Quadratics In Standard Form

Completing the 12 1 graphing quadratics in standard form involves a systematic approach:

Identify the quadratic equation in standard form: y = ax² + bx + c.
Calculate the vertex using x = -b/(2a).
Substitute the x-value of the vertex back into the equation to find the y-coordinate.
Determine the axis of symmetry, which is x = -b/(2a).
Choose additional x-values to plot points, calculating their corresponding y-values.
Sketch the parabola, ensuring it opens upwards if a is positive or downwards if a is negative.

Key elements of the 12 1 Graphing Quadratics In Standard Form

Several key elements define the 12 1 graphing quadratics in standard form:

Vertex: The highest or lowest point of the parabola, crucial for graphing.
Axis of symmetry: A vertical line that divides the parabola into two mirror-image halves.
Direction of opening: Determined by the sign of a; positive opens upward, negative opens downward.
Y-intercept: The point where the graph intersects the y-axis, found by evaluating the equation at x = 0.

Examples of using the 12 1 Graphing Quadratics In Standard Form

Examples of the 12 1 graphing quadratics in standard form illustrate its practical application:

For the equation y = 2x² + 4x + 1, the vertex can be calculated, and the parabola can be sketched accordingly.
In the case of y = -3x² + 6x - 2, the negative coefficient indicates the parabola opens downward, affecting the graph's shape.
Using y = x² - 5, the y-intercept is easily identified as (0, -5), providing a starting point for graphing.

Quick guide on how to complete standard form graphing

Forget about scanning and printing out forms. Use our detailed instructions to fill out and eSign your documents online.

Complete standard form graphing effortlessly on any device

Online document management has become increasingly popular among organizations and individuals. It offers an ideal eco-friendly alternative to conventional printed and signed documents, as you can find the necessary form and securely save it online. airSlate SignNow provides all the tools necessary to create, modify, and eSign your documents swiftly without delays. Manage 12 1 graphing quadratics in standard form on any device with airSlate SignNow Android or iOS applications and enhance any document-centered process today.

The easiest way to modify and eSign standard form graphing with ease

Find 12 1 graphing quadratics in standard form answer key and click Get Form to begin.
Utilize the tools we offer to complete your document.
Emphasize important sections of the documents or obscure sensitive information with tools that airSlate SignNow provides specifically for this purpose.
Create your signature with the Sign tool, which takes only seconds and holds the same legal authority as a traditional ink signature.
Review the details and click on the Done button to save your modifications.
Select how you wish to share your form, via email, text message (SMS), or invitation link, or download it to your computer.

Forget about lost or misplaced documents, tedious form searching, or errors that necessitate printing new document copies. airSlate SignNow addresses your document management needs within a few clicks from any device of your choice. Modify and eSign 12 1 graphing quadratics in standard form and ensure effective communication at any stage of your form preparation process with airSlate SignNow.

be ready to get more

Create this form in 5 minutes or less

Create this form in 5 minutes!

Use professional pre-built templates to fill in and sign documents online faster. Get access to thousands of forms.

How to create an eSignature for the 12 1 graphing quadratics in standard form

Speed up your business’s document workflow by creating the professional online forms and legally-binding electronic signatures.

How to create an electronic signature for a PDF online

How to create an electronic signature for a PDF in Google Chrome

How to create an e-signature for signing PDFs in Gmail

How to create an e-signature right from your smartphone

How to create an e-signature for a PDF on iOS

How to create an e-signature for a PDF on Android

How to create an electronic signature for a PDF online

Are you looking for universal solution to eSign standard form graphing? airSlate SignNow features simplicity of use, affordability and safety in one online tool, all without the need of forcing extra software on you. You just need smooth web connection as well as a device to work on.

Keep to the step-by-step guidelines below to add an eSignature to your standard form graphing answer key:

Find the paper you need to eSign and click the Upload button.
Select My Signature.
Decide on what kind of eSignature to generate. You will find 3 variants; a drawn, uploaded or typed signature.
Make your e-autograph and click the OK button.
Choose Done.

After that, your 12 1 graphing quadratics in standard form is ready. All you must do is save it or send it by means of email. airSlate SignNow helps make eSigning much easier and a lot more hassle-free because it offers users a range of extra features like Merge Documents, Invite to Sign, Add Fields, etc. And because of its cross-platform nature, airSlate SignNow can be used on any device, personal computer or smartphone, irrespective of the OS.

How to create an electronic signature for a PDF in Google Chrome

Google Chrome’s internet browser has gained its worldwide popularity due to its number of helpful features, extensions and integrations. As an example, internet browser extensions make it possible to keep all the tools you want a click away. With the collaboration between airSlate SignNow and Google Chrome, find its extension in the Web Store and then use it to eSign standard form graphing directly in your internet browser.

The steps listed below will allow you to generate an eSignature for signing standard form graphing answer key in Google Chrome:

Find the extension Google Web Store and select Add.
Log in to your registered profile.
Click the link to the link to the paper you want to eSign and choose Open in airSlate SignNow.
Use My Signature to make your personal eSignature.
Put it anywhere on the document and then click Done.

As soon as you have done away with putting your signature on your 12 1 graphing quadratics in standard form, decide what you wish to do next - download it or share the document with other people. The airSlate SignNow extension offers you a variety of features (merging PDFs, adding numerous signers, and so on) for a better signing experience.

How to create an e-signature for signing PDFs in Gmail

Because of the fact that many businesses have already gone paperless, the vast majority of are sent by means of email. That goes for contracts and agreements, tax forms and virtually any other document that requires a signature. The question arises ‘How can I sign the standard form graphing I got right from my Gmail without any third-party apps? ’ The answer is clear - choose the airSlate SignNow Chrome extension.

Here are 5 simple steps to get your standard form graphing answer key electronically signed without leaving your Gmail profile:

Go to the Chrome Web Store and add the airSlate SignNow extension to the browser.
Sign in to the account you’ve created.
Click the electronic mail you got that includes the papers that need signing.
Choose Sign from the solution’s sidebar and make your electronic signature.
Click the Done button and the electronic signature is ready. The eSigned paper is going to be connected to the draft email made by airSlate SignNow’s eSignature solution.

The sigNow extension was created to help active people such as you to decrease the stress of signing documents. Begin putting your signature on 12 1 graphing quadratics in standard form by means of tool and become one of the millions of satisfied clients who’ve previously experienced the benefits of in-mail signing.

How to create an e-signature right from your smartphone

Mobile devices like mobile phones and tablet PCs actually are a complete business replacement for laptop and desktop computers. You are able to take them everywhere and use them while on the run providing you have got a stable internet connection. For that reason, the airSlate SignNow online application is essential for filling out and signing standard form graphing on the run. Within minutes, get an electronic document with a fully legal eSignature.

Get standard form graphing answer key eSigned straight from your mobile phone using these 6 tips:

Type signnow.com in the phone’s internet browser and log in to your account. Get registered if you don’t have an account yet.
Look for the form you need to eSign from your device and upload it.
Open the doc and select the page that should be eSigned.
Hit the My Signature button.
Create your eSignature, and apply it to the page.
Check that everything’s OK and press Done.

The entire process can last a few seconds. As a result, you can download the signed 12 1 graphing quadratics in standard form to your device or share it with other parties involved with a link or by email. Because of its universal nature, airSlate SignNow works on any gadget and any operating system. Select our eSignature solution and forget about the old days with affordability, efficiency and security.

How to create an e-signature for a PDF on iOS

In case you own an iOS device like an iPad or iPhone, easily create electronic signatures for signing a standard form graphing in PDF file format. airSlate SignNow has taken care of iOS users and came up with an application only for them. To find it, visit the AppStore and type airSlate SignNow in the search field.

To sign a standard form graphing answer key right from your iPad or iPhone, just keep to these brief guidelines:

Install the airSlate SignNow application on the iOS device.
Make an account using your email or register via Facebook or Google.
Import the PDF you must eSign. Achieve that by pulling it from the cloud or the internal storage.
Pick the area you want to sign and click on Insert Initials or Insert Signature.
Draw your initials or signature, put it in the corresponding field and save the changes.

As soon as it’s signed it’s your decision regarding how to export your 12 1 graphing quadratics in standard form: save it to your mobile device, upload it to the cloud storage or send it to other people via e-mail. The airSlate SignNow mobile app is as efficient and powerful as the online tool is. Get connected to a smooth web connection and begin executing documents with a legally-binding eSignature in minutes.

How to create an e-signature for a PDF on Android

Despite iOS devices being very popular among mobile phone users, the market share of Android gadgets is a lot bigger. For that reason, airSlate SignNow has developed a separate app for mobiles working on the Android operating system. Find the application in the Play Market and set it up for putting your electronic signature on your standard form graphing.

To be able to add an e- signature to a standard form graphing answer key, keep to the simple recommendations below:

Log in to your airSlate SignNow account. In case you haven’t created it yet, you are able to do it, by means of Google or Facebook.
Add the PDF file you want to eSign using your camera or cloud storage by simply clicking on the + icon.
Find the place in which you need to add your eSignature and then draw it right in the popup window.
Click OK and place it by simply clicking the ✓ icon and then save the modifications.
Download the resulting file.

If you need to share the 12 1 graphing quadratics in standard form with other parties, it is possible to send it by e-mail. With airSlate SignNow, you are able to eSign as many documents per day as you require at a reasonable price. Start automating your signature workflows today.

Get more for 12 1 graphing quadratics in standard form

Find out other standard form graphing

be ready to get more

Get this form now!

If you believe that this page should be taken down, please follow our DMCA take down process here.

12 1 Graphing Quadratics in Standard Form

How it works

What is the 12 1 Graphing Quadratics In Standard Form

How to use the 12 1 Graphing Quadratics In Standard Form

Steps to complete the 12 1 Graphing Quadratics In Standard Form

Key elements of the 12 1 Graphing Quadratics In Standard Form

Examples of using the 12 1 Graphing Quadratics In Standard Form

Quick guide on how to complete standard form graphing

Complete standard form graphing effortlessly on any device

The easiest way to modify and eSign standard form graphing with ease

Create this form in 5 minutes or less

Create this form in 5 minutes!

How to create an eSignature for the 12 1 graphing quadratics in standard form

How to create an electronic signature for a PDF online

How to create an electronic signature for a PDF in Google Chrome

How to create an e-signature for signing PDFs in Gmail

How to create an e-signature right from your smartphone

How to create an e-signature for a PDF on iOS

How to create an e-signature for a PDF on Android

Related links to standard form graphing

People also ask 12 1 graphing quadratics in standard form answer key

Get more for 12 1 graphing quadratics in standard form

Find out other standard form graphing

Get this form now!