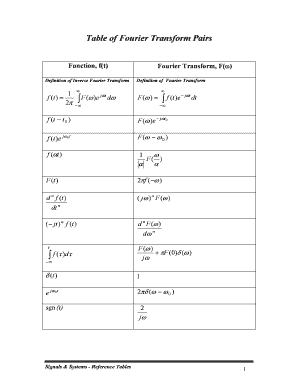
Fourier Pairs Form

What is the Fourier Pairs

The Fourier pairs refer to a set of mathematical functions that are related through the Fourier transform. This relationship allows for the conversion of a function from its time domain representation to its frequency domain representation and vice versa. In essence, a Fourier transform pair consists of a function and its corresponding transform, which captures the frequency components of the original function. Understanding these pairs is essential for various applications in engineering, physics, and signal processing, where analyzing signals in both domains is crucial.

How to use the Fourier Pairs

Using Fourier pairs involves applying the Fourier transform to a given function to analyze its frequency content. To utilize these pairs effectively, one must first identify the function to be transformed. Then, apply the appropriate Fourier transform formula to obtain its frequency representation. This process is often facilitated by software tools that can handle complex calculations. Once the frequency domain representation is obtained, it can be analyzed to extract useful information, such as identifying dominant frequencies or filtering out noise.

Steps to complete the Fourier Pairs

Completing the Fourier pairs involves several systematic steps:

• Identify the function: Begin by determining the function you wish to transform.
• Choose the appropriate Fourier transform: Select the correct type of Fourier transform based on the function's characteristics (e.g., continuous or discrete).
• Apply the transform: Use the Fourier transform formula to convert the function into its frequency domain representation.
• Analyze the results: Examine the transformed data to identify key frequency components and their significance.

Legal use of the Fourier Pairs

The legal use of Fourier pairs in various fields, particularly in digital signal processing and telecommunications, must comply with established standards and regulations. When using Fourier transforms in applications that involve data transmission or storage, it is essential to ensure that the methods employed do not infringe on intellectual property rights. Additionally, when presenting findings based on Fourier pairs in academic or professional settings, proper citations and adherence to ethical guidelines are necessary to maintain integrity and transparency.

Examples of using the Fourier Pairs

Fourier pairs are widely used in numerous applications. For instance, in audio processing, the Fourier transform can analyze sound waves to identify pitch and tone. In image processing, Fourier transforms help in filtering and enhancing images by transforming them into the frequency domain. Additionally, in communications, Fourier pairs are crucial for modulating signals for transmission over various media. These examples illustrate the versatility and importance of Fourier pairs in practical applications across different fields.

Key elements of the Fourier Pairs

Several key elements define Fourier pairs and their functionality:

• Time and frequency domains: The relationship between the time domain representation of a function and its frequency domain counterpart.
• Transform equations: The mathematical formulas that govern the transformation process.
• Properties: Characteristics such as linearity, time-shifting, and frequency-shifting that influence how functions behave under transformation.
• Inverse transforms: Methods to revert the frequency domain representation back to the time domain, ensuring the original information is preserved.