Electronic Signature
Forms Library
Other Forms
All Forms
Trigonometry Prerequisite Special Right Triangles Form

We are not affiliated with any brand or entity on this form.

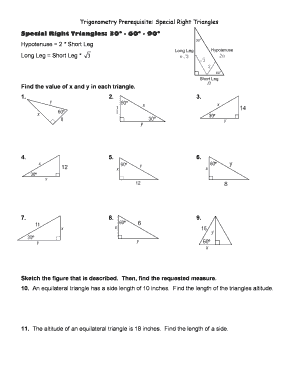
Trigonometry Prerequisite Special Right Triangles Form

Use a Trigonometry Prerequisite Special Right Triangles template to make your document workflow more streamlined.

How it works

Open form follow the instructions

Easily sign the form with your finger

Send filled & signed form or save

What makes the special right triangles 30 60 90 worksheet answers legally binding?

As the society ditches in-office working conditions, the completion of documents more and more occurs electronically. The special right triangles worksheet answer key isn’t an any different. Working with it utilizing digital tools is different from doing this in the physical world.

An eDocument can be considered legally binding given that particular needs are met. They are especially crucial when it comes to stipulations and signatures related to them. Entering your initials or full name alone will not guarantee that the organization requesting the form or a court would consider it performed. You need a trustworthy tool, like airSlate SignNow that provides a signer with a digital certificate. Furthermore, airSlate SignNow keeps compliance with ESIGN, UETA, and eIDAS - key legal frameworks for eSignatures.

How to protect your special right triangles worksheet pdf when completing it online?

Compliance with eSignature regulations is only a portion of what airSlate SignNow can offer to make form execution legal and safe. It also gives a lot of opportunities for smooth completion security smart. Let's rapidly run through them so that you can be assured that your special right triangle 30 60 90 worksheet answers remains protected as you fill it out.

SOC 2 Type II and PCI DSS certification: legal frameworks that are established to protect online user data and payment information.
FERPA, CCPA, HIPAA, and GDPR: leading privacy regulations in the USA and Europe.
Dual-factor authentication: provides an extra layer of security and validates other parties' identities through additional means, such as a Text message or phone call.
Audit Trail: serves to capture and record identity authentication, time and date stamp, and IP.
256-bit encryption: sends the information safely to the servers.

Filling out the right triangle trigonometry worksheet with answers pdf with airSlate SignNow will give better confidence that the output template will be legally binding and safeguarded.

Quick guide on how to complete right triangle trigonometry worksheet with answers pdf

Forget about scanning and printing out forms. Use our detailed instructions to fill out and eSign your documents online.

Effortlessly Prepare special right triangles 30 60 90 worksheet on Any Device

Managing documents online has gained traction among both businesses and individuals. It offers an ideal environmentally friendly alternative to conventional printed and signed documents, as you can easily locate the correct form and securely store it online. airSlate SignNow provides all the tools necessary to create, modify, and electronically sign your documents quickly and smoothly. Handle special right triangles worksheet answers on any device with airSlate SignNow's Android or iOS applications and simplify any document-related task today.

How to Modify and Electronically Sign trigonometry prerequisite special right triangles worksheet with Ease

Obtain special right triangles answer key and click on Get Form to begin.
Utilize the tools we offer to complete your form.
Highlight important sections of your documents or redact sensitive information with tools specifically provided by airSlate SignNow.
Create your eSignature with the Sign feature, which takes mere seconds and holds the same legal validity as a traditional handwritten signature.
Review the data and click on the Done button to retain your modifications.
Choose your preferred method to send your form, whether by email, SMS, or invite link, or download it to your computer.

Eliminate concerns about lost or misplaced documents, cumbersome form searches, or mistakes that necessitate printing new document copies. airSlate SignNow meets your document management needs in just a few clicks from any device you prefer. Alter and electronically sign special right triangles 30 60 90 answers and ensure effective communication at every stage of the form preparation process with airSlate SignNow.

be ready to get more

Create this form in 5 minutes or less

Video instructions and help with filling out and completing Trigonometry Prerequisite Special Right Triangles Form

Find a suitable template on the Internet. Read all the field labels carefully. Start filling out the blanks according to the instructions:

Instructions and help about special right triangles 30 60 90 worksheet

well hi there thank you for showing up for your learning everybody uh today we embark on a new unit separated but uh I am there in spirit and I am there with my digital presence to take you through the trigonometric uh prerequisite skills that you're going to need for success in this unit so go ahead and follow along and we'll fill in the necessary background and remind you of some of the review that you would have done before so uh first we'll start with the trigonometric ratios and we have to be comfortable with these definitions these ways of talking about the sides of triangles this angle down here we've labeled this angle here Theta normally I would put that Theta inside there this diagram had it outside and then um we're thinking about that angle that angle is called the angle of Interest because that's the one we're interested in right now there's a right angle in this triangle and so that allows us to use right ang

Create this form in 5 minutes!

Use professional pre-built templates to fill in and sign documents online faster. Get access to thousands of forms.

How to create an eSignature for the special right triangles 30 60 90 answers

Speed up your business’s document workflow by creating the professional online forms and legally-binding electronic signatures.

How to create an electronic signature for a PDF online

How to create an electronic signature for a PDF in Google Chrome

How to create an e-signature for signing PDFs in Gmail

How to create an e-signature right from your smartphone

How to create an e-signature for a PDF on iOS

How to create an e-signature for a PDF on Android

How to create an electronic signature for a PDF online

Do you need a one-size-fits-all solution to electronically sign special right triangles 30 60 90 worksheet answers? airSlate SignNow brings together simplicity of use, affordable price and security in one online tool, all without the need of forcing extra applications on you. All you need is reliable internet access and a gadget to work on.

Keep to the step-by-step recommendations listed below to add an eSignature to your special right triangles worksheet answer key:

Choose the document you want to sign and click on the Upload button.
Click the My Signature button.
Decide on what kind of electronic signature to generate. You will find 3 options; a drawn, typed or uploaded eSignature.
Create your eSignature and click on Ok.
Hit the Done button.

Now, your special right triangles worksheet pdf is ready. All you have to do is save it or send it by means of email. airSlate SignNow helps make eSigning easier and a lot more convenient as it provides users with a number of additional features like Merge Documents, Add Fields, Invite to Sign, etc. And due to its cross-platform nature, airSlate SignNow works well on any gadget, desktop computer or mobile phone, regardless of the OS.

How to create an electronic signature for a PDF in Google Chrome

Google Chrome’s browser has acquired its worldwide popularity because of its number of useful functions, extensions and integrations. For example, browser extensions have the ability to maintain all of the tools you need a click away. Due to the cooperation between airSlate SignNow and Google Chrome, easily find its extension in the Web Store and then use it to electronically sign special right triangles 30 60 90 worksheet answers directly in your browser.

The steps below will enable you to create an electronic signature for signing special right triangles worksheet answer key in Google Chrome:

Browse for the extension Google Web Store and push Add.
Sign in to your registered account.
Click on the link to the link to the paper you want to eSign and select Open in airSlate SignNow.
Use the My Signature tool to generate a unique electronic signature.
Put it anywhere on the page and click on Done.

Once you have done away with signing your special right triangles worksheet pdf, choose what you want to do next - download it or share the file with other people. The airSlate SignNow extension offers you a variety of features (merging PDFs, including multiple signers, and many others) to guarantee a much better signing experience.

How to create an e-signature for signing PDFs in Gmail

Because of the fact that many organizations have gone paperless, papers are delivered through e-mail. That goes for agreements and contracts, legal forms and virtually any other paper which requires a signature. The question arises ‘How can I eSign the special right triangles 30 60 90 worksheet answers I received straight from my Gmail without using third-party apps? ’ The answer is clear - use the airSlate SignNow extension for Chrome.

Here are several simple steps to get your special right triangles worksheet answer key eSigned without the need to leave your Gmail profile:

Go to the Google Chrome Web Store and add the airSlate SignNow extension to the internet browser.
Log in to your account.
Click on the email you received with the documents that require signing.
Choose the Sign option in the solution’s sidebar and create your electronic signature.
Press the Done button and your eSignature is ready. The eSigned paper will be attached to the draft electronic mail created by airSlate SignNow’s eSignature solution.

The sigNow extension was designed to help busy people such as you to decrease the burden of signing legal forms. Begin eSigning special right triangles worksheet pdf by means of tool and join the numerous satisfied clients who’ve already experienced the benefits of in-mail signing.

How to create an e-signature right from your smartphone

Portable devices like mobile phones and tablet PCs are actually a ready business alternative to desktop and laptop computers. You can carry them everywhere and use them on the run as long as you have a stable connection to the internet. For that reason, the airSlate SignNow web application is important for filling out and putting your signature on special right triangles 30 60 90 worksheet answers on the run. In a matter of seconds, receive an digital paper with a court-admissible eSignature.

Get special right triangles worksheet answer key eSigned right from your mobile phone following these six tips:

Enter signnow.com in your phone’s internet browser and log in to your account. If you don’t have an account yet, register.
Find the paper you need to eSign from your gadget and upload it.
Open the document and select the page which needs to be eSigned.
Click the My Signature button.
Create your electronic signature, and apply it to the page.
Check that everything’s OK and hit the Done button.

The whole process can last less than a minute. As a result, you can download the signed special right triangles worksheet pdf to your device or share it with other parties involved with a link or by email. Because of its universal nature, airSlate SignNow works on any gadget and any operating system. Choose our eSignature tool and forget about the old days with affordability, efficiency and security.

How to create an e-signature for a PDF on iOS

In case you use an iOS device like an iPhone or iPad, effortlessly generate e- signatures for signing a special right triangles 30 60 90 worksheet answers in PDF formatting. airSlate SignNow has taken care of iOS users and came up with an app only for them. To get it, visit the AppStore and enter airSlate SignNow in the search field.

To eSign a special right triangles worksheet answer key right from your iPhone or iPad, just stick to these simple instructions:

Set up the airSlate SignNow application on your iOS device.
Create an account with your email or log in via Facebook or Google.
Import the PDF document you have to eSign. Do this by pulling it from the cloud or the internal storage.
Choose the area you need to eSign and click on Insert Initials or Insert Signature.
Draw your initials or signature, insert it in the corresponding field and save the changes.

After it is signed it is up to you concerning how to export your special right triangles worksheet pdf: save it to your mobile device, add it to the cloud storage or send it to another party using email. The airSlate SignNow application is as productive and powerful as the online app is. Connect to a strong connection to the internet and start executing forms with a fully legitimate electronic signature in minutes.

How to create an e-signature for a PDF on Android

In spite of iPhones being very popular with mobile users, the market share of Android OS smartphones and tablets is much greater. For that reason, airSlate SignNow provides a specialized application for mobiles working on the Android operating system. Find the app in the Play Market and set it up for eSigning your special right triangles 30 60 90 worksheet answers.

To add an electronic autograph to a special right triangles worksheet answer key, follow the step-by-step instructions below:

Log in to your airSlate SignNow profile. In case you haven’t made it yet, it is possible to be done, via Facebook or Google.
Upload the PDF file you need to work with by means of your camera or cloud storage by selecting the + icon.
Pick the place where you need to insert your electronic signature after which draw it right in the popup window.
Click OK and place it by choosing the ✓ icon after which save the changes.
Save the signed document.

If you have to share the special right triangles worksheet pdf with other people, you can easily send it by e-mail. With airSlate SignNow, you can eSign as many papers in a day as you need at a reasonable price. Begin automating your eSignature workflows right now.

Get more for trigonometry prerequisite special right triangles worksheet answers

Find out other special right triangles

be ready to get more

Get this form now!

If you believe that this page should be taken down, please follow our DMCA take down process here.

Trigonometry Prerequisite Special Right Triangles Form

How it works

What makes the special right triangles 30 60 90 worksheet answers legally binding?

How to protect your special right triangles worksheet pdf when completing it online?

Quick guide on how to complete right triangle trigonometry worksheet with answers pdf

Effortlessly Prepare special right triangles 30 60 90 worksheet on Any Device

How to Modify and Electronically Sign trigonometry prerequisite special right triangles worksheet with Ease

Create this form in 5 minutes or less

Video instructions and help with filling out and completing Trigonometry Prerequisite Special Right Triangles Form

Instructions and help about special right triangles 30 60 90 worksheet

Related searches to special right triangles answer key

Create this form in 5 minutes!

How to create an eSignature for the special right triangles 30 60 90 answers

How to create an electronic signature for a PDF online

How to create an electronic signature for a PDF in Google Chrome

How to create an e-signature for signing PDFs in Gmail

How to create an e-signature right from your smartphone

How to create an e-signature for a PDF on iOS

How to create an e-signature for a PDF on Android

Related links to trigonometry prerequisite special right triangles worksheet pdf

Get more for trigonometry prerequisite special right triangles worksheet answers

Find out other special right triangles

Get this form now!