Electronic Signature
Forms Library
Other Forms
All Forms
QUADRIC SURFACES Name Equation in Standard Form X Const Math Ubc

We are not affiliated with any brand or entity on this form.

QUADRIC SURFACES Name Equation in Standard Form X Const Math Ubc

Use a quadratic surfaces template to make your document workflow more streamlined.

How it works

Open form follow the instructions

Easily sign the form with your finger

Send filled & signed form or save

Understanding the quadric surfaces name equation in standard form

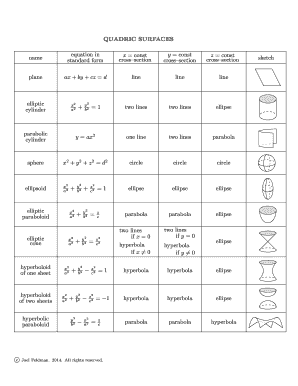
The quadric surfaces name equation in standard form is a mathematical representation that describes various types of quadric surfaces. These surfaces include ellipsoids, hyperboloids, and paraboloids, each defined by specific equations. The standard form typically takes the shape of an equation involving variables x, y, and z, allowing for a clear interpretation of the surface's geometry. For instance, the equation for an ellipsoid can be expressed as (x^2/a^2) + (y^2/b^2) + (z^2/c^2) = 1, where a, b, and c are constants determining the dimensions of the ellipsoid.

Steps to complete the quadric surfaces name equation in standard form

Completing the quadric surfaces name equation involves several steps. First, identify the type of quadric surface you are dealing with based on its properties. Next, gather the necessary parameters, such as the coefficients and constants relevant to the surface's shape. Once you have this information, substitute the values into the standard equation format. Finally, simplify the equation to ensure it is in the correct standard form. This process allows for accurate representation and analysis of the quadric surface.

Examples of using the quadric surfaces name equation in standard form

Examples of the quadric surfaces name equation in standard form can illustrate its application in various contexts. For instance, the equation for a hyperboloid of one sheet can be written as (x^2/a^2) + (y^2/b^2) - (z^2/c^2) = 1. This equation is useful in fields such as physics and engineering, where understanding the shape and properties of these surfaces is crucial. Another example is the paraboloid, represented by the equation z = (x^2/a^2) + (y^2/b^2), which is often used in optics and satellite dish design.

Legal use of the quadric surfaces name equation in standard form

The legal use of the quadric surfaces name equation in standard form pertains to its application in various regulatory and compliance contexts. For example, when presenting mathematical models in patent applications or scientific research, it is essential to ensure that the equations are accurately represented and comply with relevant standards. This accuracy helps in establishing the validity of the work and can be crucial in legal situations where intellectual property rights are concerned.

Key elements of the quadric surfaces name equation in standard form

Key elements of the quadric surfaces name equation include the variables x, y, and z, which represent the coordinates in three-dimensional space. Additionally, the constants a, b, and c are critical as they determine the shape and size of the surface. Understanding these elements is vital for anyone working with quadric surfaces, as they provide the necessary framework for analysis and application in various scientific and engineering fields.

Quick guide on how to complete types of quadric surfaces

Forget about scanning and printing out forms. Use our detailed instructions to fill out and eSign your documents online.

Prepare types of quadric surfaces effortlessly on any device

Virtual document management has become increasingly preferred by organizations and individuals. It offers an ideal eco-conscious substitute for conventional printed and signed papers, as you can locate the desired form and securely archive it online. airSlate SignNow equips you with all the necessary tools to create, modify, and eSign your documents quickly and without interruptions. Manage quadratic surfaces across any platform with airSlate SignNow Android or iOS applications and simplify any document-oriented task today.

How to modify and eSign quadric surfaces with ease

Locate equations of surfaces and click on Get Form to begin.
Use the tools we offer to finalize your form.
Emphasize pertinent sections of the documents or obscure sensitive information with tools that airSlate SignNow provides specifically for that purpose.
Create your eSignature using the Sign tool, which takes moments and has the same legal validity as a conventional wet ink signature.
Review the information and click on the Done button to save your modifications.
Select how you wish to send your form, via email, text message (SMS), or invitation link, or download it to your computer.

Eliminate the hassle of missing or lost documents, tedious form searching, or errors that necessitate printing new document copies. airSlate SignNow addresses your document management needs in just a few clicks from any device you prefer. Edit and eSign quadric surfaces equations and ensure effective communication at any point of the form preparation process with airSlate SignNow.

be ready to get more

Create this form in 5 minutes or less

Create this form in 5 minutes!

Use professional pre-built templates to fill in and sign documents online faster. Get access to thousands of forms.

How to create an eSignature for the types of quadric surfaces

Speed up your business’s document workflow by creating the professional online forms and legally-binding electronic signatures.

How to create an electronic signature for a PDF online

How to create an electronic signature for a PDF in Google Chrome

How to create an e-signature for signing PDFs in Gmail

How to create an e-signature right from your smartphone

How to create an e-signature for a PDF on iOS

How to create an e-signature for a PDF on Android

How to create an electronic signature for a PDF online

Are you looking for universal solution to electronically sign quadratic surfaces? airSlate SignNow features simplicity of use, affordable price and security in one online tool, all without forcing extra software programs on you. You only need reliable connection to the internet as well as a device to work on.

Follow the step-by-step instructions listed below to add an eSignature to your quadric surfaces:

Choose the paper you need to sign and then click the Upload button.
Choose the My Signature button.
Choose what type of eSignature to generate. You can find 3 options; a drawn, uploaded or typed eSignature.
Create your e-autograph and then click the OK button.
Select Done.

Now, your equations of surfaces is completed. All you need to do is download it or send the document by means of electronic mail. airSlate SignNow can make eSigning easier and a lot more convenient since it offers users numerous extra features like Merge Documents, Invite to Sign, Add Fields, and many others. And due to its cross-platform nature, airSlate SignNow works well on any device, PC or smartphone, irrespective of the operating system.

How to create an electronic signature for a PDF in Google Chrome

Google Chrome’s internet browser has gained its worldwide popularity due to the variety of helpful features, extensions and integrations. For example, internet browser extensions make it possible to keep all of the tools you want a click away. Due to the cooperation between airSlate SignNow and Chrome, easily find its extension in the Web Store and then use it to eSign quadratic surfaces directly in your internet browser.

The guidelines below will enable you to create an eSignature for signing quadric surfaces in Chrome:

Browse for the extension in the Web Store and push the Add button.
Sign in to your registered account.
Click on the link to the link to the file you need to eSign and select Open in airSlate SignNow.
Use the My Signature tool to create your personal eSignature.
Put it anywhere on the document and then click Done.

As soon as you’ve completed putting your signature on your equations of surfaces, choose what you should do after that - save it or share the file with other parties involved. The airSlate SignNow extension gives you a variety of features (merging PDFs, adding numerous signers, etc.) to guarantee a better signing experience.

How to create an e-signature for signing PDFs in Gmail

Due to the fact that many businesses have already gone digital, nearly all {documents are delivered through electronic mail. That applies to contracts and agreements, tax forms and virtually any other document that requires a signature. The issue arises ‘How can I eSign the quadratic surfaces I got right from my Gmail with no third-party apps? ’ The answer is simple - use the airSlate SignNow Chrome extension.

Here are 5 easy steps to get your quadric surfaces eSigned without leaving your Gmail account:

Visit the Google Chrome Web Store and add the airSlate SignNow extension to your browser.
Sign in to your profile.
Click on the electronic mail you got that includes the papers that require signing.
Pick the Sign option in the solution’s sidebar and make your eSignature.
Click Done and your signature is created. The eSigned document will be connected to the draft email created by airSlate SignNow’s eSignature tool.

The sigNow extension was made to help active people like you to decrease the burden of signing legal forms. Begin putting your signature on equations of surfaces using our tool and join the millions of satisfied customers who’ve previously experienced the benefits of in-mail signing.

How to create an e-signature right from your smartphone

Portable devices like smartphones and tablet PCs are in fact a complete business substitute for desktop and laptop computers. You can take them everywhere and even use them while on the move providing you have a stable connection to the web. Consequently, the airSlate SignNow web app is a must-have for completing and signing quadratic surfaces on the move. In a matter of moments, receive an electronic paper with a court-admissible eSignature.

Get quadric surfaces eSigned from your mobile phone using these six tips:

Type signnow.com in the phone’s web browser and sign in to your profile. If you don’t have an account yet, register.
Search for the document you want to electronically sign from your gadget and upload it.
Open the file and choose the page that needs to be eSigned.
Choose the My Signature button.
Create your electronic signature, and apply it to the page.
Double-check that everything’s OK and click Done.

The whole procedure can take a few seconds. As a result, you can download the signed equations of surfaces to your device or share it with other parties involved with a link or by email. Because of its cross-platform nature, airSlate SignNow is compatible with any device and any OS. Select our eSignature solution and leave behind the old days with security, affordability and efficiency.

How to create an e-signature for a PDF on iOS

If you use an iOS device like an iPad or iPhone, easily generate e- signatures for signing a quadratic surfaces in PDF formatting. airSlate SignNow has paid close attention to iOS users and created an application just for them. To find it, visit the AppStore and type airSlate SignNow in the search field.

To eSign a quadric surfaces from your iPad or iPhone, just stick to these short recommendations:

Install the airSlate SignNow application on the iOS device.
Make a free account using your electronic mail or sign in by means of Google or Facebook.
Upload the PDF you have to eSign. Do this by getting it out of the cloud or the internal storage.
Pick the place you want to eSign and click Insert Initials or Insert Signature.
Draw your signature or initials, put it in the related box and save the changes.

Right after it is eSigned it is up to you on how to export your equations of surfaces: save it to the mobile phone, upload it to the cloud or send it to other people using e-mail. The airSlate SignNow application is just as productive and powerful as the online app is. Connect to a smooth web connection and begin completing forms with a fully legitimate eSignature in minutes.

How to create an e-signature for a PDF on Android

In spite of iPhones being very popular with mobile users, the market share of Android smartphones and tablets is significantly bigger. For that reason, airSlate SignNow offers a separate app for mobiles working on Android. Find the mobile app in the Play Market and set it up for putting your signature on your quadratic surfaces.

In order to add an e- signature to your quadric surfaces, follow the step-by-step instructions listed below:

Log in to your airSlate SignNow account. In case you have not created one yet, you can, by means of Google or Facebook.
Upload the PDF you want to work with by means of your camera or cloud storage by simply clicking on the + symbol.
Pick the place in which you would like to put your electronic signature after which draw it in the popup window.
Confirm and place it by clicking on the ✓ symbol after which save the changes.
Download the eSigned document.

If you need to share the equations of surfaces with other parties, it is possible to send it by electronic mail. With airSlate SignNow, you are able to eSign as many papers in a day as you need at an affordable price. Begin automating your signature workflows right now.

Get more for equations of surfaces

Find out other quadric surfaces equations

be ready to get more

Get this form now!

If you believe that this page should be taken down, please follow our DMCA take down process here.

QUADRIC SURFACES Name Equation in Standard Form X Const Math Ubc

How it works

Understanding the quadric surfaces name equation in standard form

Steps to complete the quadric surfaces name equation in standard form

Examples of using the quadric surfaces name equation in standard form

Legal use of the quadric surfaces name equation in standard form

Key elements of the quadric surfaces name equation in standard form

Quick guide on how to complete types of quadric surfaces

Prepare types of quadric surfaces effortlessly on any device

How to modify and eSign quadric surfaces with ease

Create this form in 5 minutes or less

Create this form in 5 minutes!

How to create an eSignature for the types of quadric surfaces

How to create an electronic signature for a PDF online

How to create an electronic signature for a PDF in Google Chrome

How to create an e-signature for signing PDFs in Gmail

How to create an e-signature right from your smartphone

How to create an e-signature for a PDF on iOS

How to create an e-signature for a PDF on Android

Related links to quadratic surfaces

People also ask quadric surfaces

Get more for equations of surfaces

Find out other quadric surfaces equations

Get this form now!