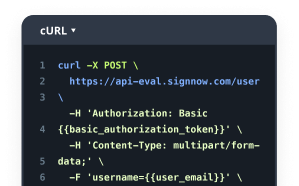
Unlock the Full Potential of Digital Signature Lawfulness for R&D in India with airSlate SignNow

Digital Signature Lawfulness for R&D in India

In the rapidly evolving landscape of technology and research, ensuring the legality of digital signatures is crucial for R&D activities in India. Compliance with digital signature laws is essential to maintain the integrity and authenticity of documents exchanged in the research field.

airSlate SignNow Benefits

• Launch the airSlate SignNow web page in your browser.
• Sign up for a free trial or log in.
• Upload a document you want to sign or send for signing.
• If you're going to reuse your document later, turn it into a template.
• Open your file and make edits: add fillable fields or insert information.
• Sign your document and add signature fields for the recipients.
• Click Continue to set up and send an eSignature invite.

airSlate SignNow empowers businesses to send and eSign documents with an easy-to-use, cost-effective solution. It offers great ROI with a rich feature set, scalability tailored for SMBs and Mid-Market companies, transparent pricing without hidden fees, and superior 24/7 support for all paid plans.

Experience the benefits of airSlate SignNow for your document signing needs today!

What is the digital signature lawfulness for rd in india

The digital signature lawfulness for rd in india refers to the legal recognition of electronic signatures within the context of regulatory documents. This framework ensures that digital signatures are considered valid and enforceable, similar to traditional handwritten signatures. The law establishes guidelines for the use of digital signatures in various transactions, providing a secure method for verifying the identity of signers and the integrity of the signed documents.

How to use the digital signature lawfulness for rd in india

Utilizing the digital signature lawfulness for rd in india involves several steps. Users must first ensure that the digital signature complies with the relevant legal standards. This includes obtaining a digital certificate from a recognized certifying authority. Once the certificate is secured, users can apply their digital signature to documents electronically. This process typically involves uploading the document to an eSignature platform, selecting the appropriate signature option, and confirming the signing action. The completed document can then be securely shared or stored.

Steps to complete the digital signature lawfulness for rd in india

To complete the digital signature lawfulness for rd in india, follow these steps:

• Obtain a digital certificate from an accredited certifying authority.
• Choose an eSignature platform, such as airSlate SignNow, to manage your documents.
• Upload the document that requires signing.
• Select the area where the signature is needed and apply your digital signature.
• Review the document for accuracy before finalizing the signature.
• Save and securely share the signed document with relevant parties.

Legal use of the digital signature lawfulness for rd in india

The legal use of the digital signature lawfulness for rd in india is governed by specific regulations that outline acceptable practices. These regulations ensure that digital signatures are used in a manner that protects the interests of all parties involved. Compliance with these laws is essential for the enforceability of electronically signed documents. Users should familiarize themselves with the legal requirements to ensure their digital signatures meet the necessary standards.

Security & Compliance Guidelines

Security and compliance are critical when using digital signatures. Users should adopt best practices to protect sensitive information and ensure the integrity of signed documents. This includes using strong passwords for digital certificates, ensuring that eSignature platforms comply with industry standards, and regularly updating security protocols. Additionally, users should maintain records of all signed documents for compliance and auditing purposes.

Documents You Can Sign

With the digital signature lawfulness for rd in india, users can sign a wide range of documents electronically. Common examples include contracts, agreements, regulatory filings, and various forms required by government agencies. The ability to eSign these documents streamlines workflows, reduces processing time, and enhances overall efficiency in handling important paperwork.