How To Integrate eSign in Box
Contact Sales
Make the most out of your eSignature workflows with airSlate SignNow
Extensive suite of eSignature tools
Robust integration and API capabilities
Advanced security and compliance
Various collaboration tools
Enjoyable and stress-free signing experience
Extensive support
Keep your eSignature workflows on track
Our user reviews speak for themselves






How to incorporate e-signatures with airSlate SignNow
If you're searching for a smooth method to handle your documents via e-signatures, discover how to incorporate e-signatures with airSlate SignNow. This platform enables organizations to send and sign documents effortlessly, providing an economical solution designed for small to medium-sized businesses. With its intuitive interface and comprehensive feature set, airSlate SignNow is built to improve your document management experience.
How to incorporate e-signatures with airSlate SignNow
- Launch your web browser and go to the airSlate SignNow homepage.
- Create a complimentary trial account or log in if you already possess an account.
- Choose the document you want to sign or send for signing by uploading it to the platform.
- If you foresee using this document again, convert it into a template for future reference.
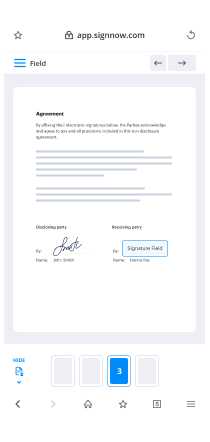
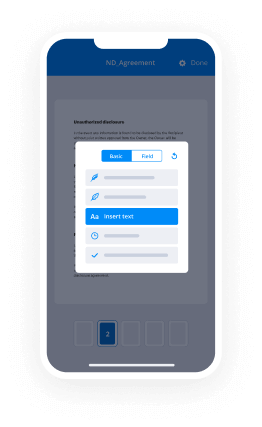
- Access your uploaded document to make necessary modifications: insert fillable fields or required data.
- Sign the document yourself and designate signature fields for the recipients.
- Click 'Continue' to set up and send the eSignature invitation.
By following these instructions, you can effectively incorporate e-signatures into your business process using airSlate SignNow. This platform not only streamlines the signing procedure but also increases productivity and collaboration.
Ready to revolutionize your document management? Sign up for airSlate SignNow today and enjoy exceptional support, clear pricing, and a powerful feature set that provides excellent ROI!
How it works
Rate your experience
-
Best ROI. Our customers achieve an average 7x ROI within the first six months.
-
Scales with your use cases. From SMBs to mid-market, airSlate SignNow delivers results for businesses of all sizes.
-
Intuitive UI and API. Sign and send documents from your apps in minutes.
A smarter way to work: —how to industry sign banking integrate
FAQs
-
How to integrate e-signatures into my existing workflow?
To integrate e-signatures into your existing workflow, airSlate SignNow provides seamless API integration options. You can easily connect your current software with SignNow to streamline document signing processes. For detailed guidance on how to integrate e, refer to our integration documentation.
-
What are the pricing options for airSlate SignNow?
airSlate SignNow offers flexible pricing plans to suit various business needs. Whether you are a small business or a large enterprise, you can find a plan that fits your budget. Visit our pricing page to learn how to integrate e-signatures at a cost-effective rate.
-
Can I customize the e-signature process?
Yes, airSlate SignNow allows you to customize the e-signature process to align with your business requirements. You can add your branding, choose signing workflows, and tailor notifications. This level of customization shows you how to integrate e-signatures effectively into your operations.
-
What features does airSlate SignNow offer for document management?
airSlate SignNow offers robust features for document management, including templates, document sharing, and real-time tracking. These tools enhance your ability to manage documents efficiently. Discover how to integrate e-signatures and document management in one cohesive platform.
-
How to integrate e-signatures with third-party applications?
Integrating e-signatures with third-party applications is straightforward with airSlate SignNow's extensive integration capabilities. You can connect with popular tools like Salesforce or Google Drive easily. Check our integration guide to learn how to integrate e-signatures with your favorite apps.
-
Is airSlate SignNow compliant with legal standards?
Absolutely! airSlate SignNow complies with all legal standards for electronic signatures, ensuring that your signed documents are legally binding. This compliance is crucial for businesses looking to understand how to integrate e-signatures responsibly.
-
What are the benefits of using airSlate SignNow for e-signatures?
Using airSlate SignNow for e-signatures offers numerous benefits, including increased efficiency, reduced turnaround times, and enhanced security. These advantages help businesses save time and resources. Learning how to integrate e-signatures into your processes can signNowly improve your overall productivity.
-
How do I integrate Salesforce with Box?
Great question! Being the CMO of cloudHQ, this is a question I think I should answer! :-) Box has an integration with Salesforce, but it really doesn't cut the mustard because: There's no automatic backup of Box in Salesforce, or of Salesforce in Box. Sorry- but you are able to do it manually. Users need to depend on 2 services: Salesforce AND Box to work. Last Sunday Box was down. What about countries where our Sunday is a Monday (Australia, Philippines, etc)? By depending on two services, you risk your work reliability. No search: All documents stay in Box, so salespeople can't search for their docs in Salesforce. The search results will show "no results". Salespeople need to hyperlink a Box doc to their chatter files or personal library, and then click the hyperlink to go to Box and access it there. The biggest issue is that these hyperlinks are (1) auto-generated by Box, so the title doesn't tell you what the document is, and (2) the title isn't searchable.Don't get me wrong, the Box cloud storage solution is PERFECT for many enterprises, but their integration lacks major functionality. So, with cloudHQ, we can map the sync for you, and you can still use Box with Salesforce.Here's how we do it:In Box, we map your Salesforce folders into 3 sections: accounts, opportunities, and your personal library (including chatter files). So whatever you put into Salesforce, gets synched to Box, in one of the 3 folders. Whatever is in your Box account is synched to the appropriate account, opportunity, and personal library in Salesforce. And I'm not talking about hyperlinks, I'm talking about the whole damn document. Because that's what salespeople need when they're on the go. They need a fast search that brings up their documents via mobile in Salesforce.Backup: Whatever is in your Salesforce will automatically appear in Box, in real-time. And whatever is in Box, will automatically appear in Salesforce. Do you have a report you need to share? Get it all in your Box folder and share the link with your supervisors. It'll always be up to date since the sync is in realtime. :)Safety with Archive folders: If you ever accidentally delete an account, or information is all of a sudden missing because of a malicious deletion, enable your archive folders in cloudHQ. It'll save a copy of your Salesforce account before any changes have been made in Box. This will give you no down time, and you can always just pick up where you left off. Give cloudHQ a whirl. Here's a 10% discount on top of your 15 day, no credit card free trial: 10% discount - cloudHQ Also, please let me know if you need more information, or if there's something else that you need that cloudHQ doesn't offer. We really want to help! :-)
-
How can you prove that [math]\displaystyle\int_{0}^{\infty}\frac{\cos (x)}{x^{2}+1}\,\mathrm dx=\frac{\pi}{2e}[/math] ?
The given integral,[math]I'=\displaystyle\int_{0}^{\infty}\dfrac{\cos (x)}{x^{2}+1}\,\mathrm dx[/math]can be evaluated with the help of complex analysis.[math]I=\frac{1}{2}\displaystyle\int_{-\infty}^{\infty}\dfrac{cos(x)}{x^{2}+1}\,\mathrm dx[/math] (Since it is even function so we changed the limits from minus infinity to plus infinity and halfed the integral.)Writing [math]cos(x)=e^{ix}[/math] ,[math]I=\frac{1}{2}\displaystyle\int_{-\infty}^{\infty}\dfrac{e^{i x}}{x^{2}+1}\,\mathrm dx[/math][math]I’[/math] is just the real part of [math]I[/math][math]\implies I=\frac{1}{2}\displaystyle\int_{-\infty}^{\infty}\dfrac{e^{i z}}{z^{2}+1}\,\mathrm dz[/math] (Since now we work in complex plane)Now, we equate[math]z^{2}+1=0[/math][math]\implies z=+i,-i[/math]Here, we take all the points lying in the upper half plane.i.e., [math]z=+i[/math]Now basically finding[math] I [/math] is finding residue of function [math]f(z)=\dfrac{e^{iz}}{z^{2}+1}[/math] at [math]z=+i[/math]So,[math]I=\dfrac{1}{2}(2\pi i) \displaystyle Res_{z = +i}f(z)[/math][math]\implies I=\dfrac{1}{2}(2\pi i)\displaystyle Res_{z = +i}\dfrac{e^{i z}}{z^{2}+1}[/math][math]\implies I=(\pi i)\displaystyle\lim_{z\to +i}(z-i)\dfrac{e^{i z}}{z^{2}+1}[/math][math]\implies I=(\pi i)\displaystyle\lim_{z\to +i}(z-i)\dfrac{e^{iz}}{(z-i)(z+i)}[/math][math]\implies I=(\pi i)\displaystyle\lim_{z\to +i}\dfrac{e^{i z}}{(z+i)}[/math][math]\implies I=(\pi i)\dfrac{e^{i.i}}{(i+i)}[/math][math]\implies I=(\pi i)\dfrac{e^{-1}}{2i}[/math][math]\implies I=(\pi)\dfrac{e^{-1}}{2}[/math][math]\implies I=(\pi)\dfrac{1}{2e}[/math][math]\implies I=\dfrac{\pi}{2e}[/math]So, real part of [math]I[/math] is[math]\dfrac{\pi}{2e} [/math] which is the required answer.Therefore,[math]\displaystyle\int_{0}^{\infty}\dfrac{\cos (x)}{x^{2}+1}\,\mathrm dx=\dfrac{\pi}{2e}[/math]I hope you liked the answer.
-
How do you use LaTeX mathematical notation for formulae on Quora?
From our Help Center article, How do you use LaTeX mathematical notation for formulae on Quora?:You can write LaTeX and have it styled correctly by using the Math formatting option in the Quora editor (see screenshot) or by using the keyboard shortcut.For more information about Quora’s features and frequently asked questions, check out our Help Center.
-
How is box.net integrated with Salesforce?
While Box.net (now Box.com) has improved their Salesforce integration, it's still rather lackluster as I write this reply. There are 3 major problems with the Box <-> Salesforce integrationHyperlinks amputate your Sales Team:Box does its basic job of allowing Box documents to be correctly mapped into Salesforce's accounts or other libraries, however those documents are represented by hyperlinks that are auto-generated gibberish names. That means that in your Salesforce account, you have to go through all of your documents to find the right one. There's no preview, and there's no logical naming system.. so if you have more than 5 documents in one account, your salespeople/customer service people are going to be spending a ridiculous amount of time trying to find the correct document.On that note, if your salespeople are on the road and need to use Salesforce's search feature to find a document, they cannot. The search feature won't help them because the document is only hyperlinked to Box; it doesn't actually live in Salesforce, and therefore the Salesforce search feature cannot search for Box documents that are hyperlinked.Two-system Dependency Danger Zone:When one system is temporarily disabled (which happens more often that you think), you're actually crippling your business from functioning because the current Box-Salesforce integration actually requires you to be dependent on both platforms simultaneously. This is a huge risk for many businesses because you should have a fail-over method in case one platform goes down. In this instance, you have no safety zone. In fact, you double your risk by having to rely on 2 platforms. Why is this happening? This has a lot to do with platforms wanting to keep your information on their platform, and theirs only, because your data is valuable. It makes you rely on their platform, and they can charge you as you use it. Manual backups:This is more of a nuisance than a major flaw, but still, it's very much a big time waster. In order to backup your Salesforce information to Box, you need to manually set up a backup. It's a big pain in the butt. ---Clearly I'm biased because I'm cloudHQ's co-founder, but I would love for you to try the Box integration with Salesforce! It'll be a great starting point for comparison with our sync service. cloudHQ replicates your Salesforce into Box in real-time and automatically, pre-mapped out for you in 4 separate folders:AccountsOpportunitiesReportsDocumentsIf you prefer to have backups throughout the day, you can also set that up as well. Furthermore, your documents will live both in Box AND in Salesforce, helping you keep a safe fail-over method in case either service is temporarily disrupted. It also therefore enables your employees to you use Salesforce's search feature easily; saving your employees' time. Lastly, there's no manual backups! It's just all backed up for you automatically, and there's a 15-day free trial.I hope this helps explain the difference between how Box and Salesforce is currently set up through Box's integration, and what you can do to optimize it through cloudHQ.Best,Naomi
-
How would you prove this? [math]\int_{0}^{\infty}\frac{\sin(t)}{t}\mathrm {d}t=\frac{\pi}{2}[/math]
This is an intriguing integral, one of the simplest in which the indefinite integral cannot be expressed in terms of elementary functions but where the definite integral is a finite and determinable quantity. There are numerous equivalent ways in which it can be resolved, and the mathematician G. H. Hardy wrote an article in the Mathematical Gazette in 1909 in which he compares a number of different approaches.I shall outline yet another method here, which relies only on conventional real integration and analysis to convert the integral of [math]\frac{\sin{t}}{t}[/math], which cannot be expressed in elementary functions, into the integral of [math]\frac{1}{u^2 + 1}[/math], which can. We will need the following results, which I’ll prove below:Lemma A: [math]\displaystyle \lim_{y \to \infty} \int_0^y e^{-tu}\sin{t} \,\mathrm du = \frac{\sin{t}}{t}[/math]Lemma B: [math]\displaystyle \int_0^x \int_0^y e^{-tu}\sin{t} \,\mathrm du \,\mathrm dt = \int_0^y \int_0^x e^{-tu}\sin{t} \,\mathrm dt \,\mathrm du[/math]Lemma C: [math]\displaystyle \lim_{x \to \infty} \int_0^x e^{-tu}\sin{t} \,\mathrm dt = \frac{1}{u^2 + 1}[/math]With these we can now tackle the integral we are interested in:[math]\begin{align} \lim_{x \to \infty} \int_0^x \frac{\sin{t}}{t} \,\mathrm dt &= \lim_{x \to \infty} \int_0^x \left( \lim_{y \to \infty} \int_0^y e^{-tu}\sin{t} \,\mathrm du \right) \,\mathrm dt && \text{by lemma A} \\ &= \lim_{x \to \infty} \lim_{y \to \infty} \int_0^x \int_0^y e^{-tu}\sin{t} \,\mathrm du \,\mathrm dt \\ &= \lim_{x \to \infty} \lim_{y \to \infty} \int_0^y \int_0^x e^{-tu}\sin{t} \,\mathrm dt \,\mathrm du && \text{by lemma B} \\ &= \lim_{y \to \infty} \int_0^y \left( \lim_{x \to \infty} \int_0^x e^{-tu}\sin{t} \,\mathrm dt \right) \,\mathrm du \\ &= \lim_{y \to \infty} \int_0^y \frac{1}{u^2 + 1} \,\mathrm du && \text{by lemma C} \\ &= \lim_{y \to \infty} \bigg[ \arctan{u}\, \bigg]_0^y \\ &= \lim_{y \to \infty} \big( \arctan{y} - \arctan{0} \big) \\ &= \lim_{y \to \infty} \arctan{y} = \frac{\pi}{2}\ \text{ QED} \end{align}[/math]Proof of lemma A: [math]\displaystyle \lim_{y \to \infty} \int_0^y e^{-tu} \sin{t} \,\mathrm du = \frac{\sin{t}}{t}[/math]Let [math]v = -tu\ \therefore \mathrm dv = -t\,\mathrm du[/math], [math]v = 0[/math] when [math]u = 0[/math] and [math]v = -ty[/math] when [math]u = y[/math].[math]\begin{align} \therefore \lim_{y \to \infty} \int_0^y e^{-tu} \sin{t} \,\mathrm du &= \lim_{y \to \infty} \int_0^{-ty} \frac{e^v \sin{t}}{-t} \,\mathrm dv \\ &= \lim_{y \to \infty} \frac{\sin{t}}{t} \int_0^{-ty} -e^v \,\mathrm dv \\ &= \frac{\sin{t}}{t} \lim_{y \to \infty} \bigg[ -e^v \bigg]_0^{-ty} \\ &= \frac{\sin{t}}{t} \lim_{y \to \infty} \left( -e^{-ty} + e^0 \right) \\ &= \frac{\sin{t}}{t}\ \text{ QED} \end{align}[/math]Proof of lemma B: [math]\displaystyle \int_0^x \int_0^y e^{-tu}\sin{t} \,\mathrm du \,\mathrm dt = \int_0^y \int_0^x e^{-tu}\sin{t} \,\mathrm dt \,\mathrm du[/math]Note that [math]0 < e^{-tu} \le 1\ \forall t,u \ge 0[/math] and [math]\left\lvert \sin{t} \right\rvert \le 1\ \forall t[/math][math]\therefore \displaystyle \int_0^x \int_0^y \left\lvert e^{-tu}\sin{t} \right\rvert \,\mathrm du \,\mathrm dt \le \int_0^x \int_0^y 1 \,\mathrm du \,\mathrm dt = xy < \infty[/math]We can therefore apply Fubini's theorem which tells us that[math]\displaystyle \int_{X \times Y} \left\lvert f(x,y) \right\rvert \mathrm d(x,y) < \infty \implies \displaystyle \int_X \int_Y f(x,y) \,\mathrm dy \,\mathrm dx = \int_Y \int_X f(x,y) \,\mathrm dx \,\mathrm dy[/math].Proof of lemma C: [math]\displaystyle \lim_{x \to \infty} \int_0^x e^{-tu}\sin{t} \,\mathrm dt = \frac{1}{u^2 + 1}[/math]Let [math]T = \displaystyle \int e^{-tu} \sin{t} \,\mathrm dt[/math]We use integration by parts, which uses the following general rule:[math]\int v\, {\normalsize \frac{\mathrm dw}{\mathrm dt}} \,\mathrm dt = vw - \int w\, {\normalsize \frac{\mathrm dv}{\mathrm dt}} \,\mathrm dt[/math]Let [math]v = e^{-tu}[/math] and [math]w = -\cos{t}[/math], so [math]{\normalsize \frac{\mathrm dv}{\mathrm dt}} = -ue^{-tu}[/math] and [math]{\normalsize \frac{\mathrm dw}{\mathrm dt}} = \sin{t}[/math].[math]\begin{align} \therefore T &= \int v\, \frac{\mathrm dw}{\mathrm dt} \,\mathrm dt \\ &= vw - \int w\, \frac{\mathrm dv}{\mathrm dt}\,\mathrm dt \\ &= -e^{-tu}\cos{t} - \int ue^{-tu}\cos{t} \,\mathrm dt \end{align}[/math]We use integration by parts again, this time with [math]v = e^{-tu}[/math] and [math]w = \sin{t}[/math], so [math]{\normalsize \frac{\mathrm dv}{\mathrm dt}} = -ue^{-tu}[/math] and [math]{\normalsize \frac{\mathrm dw}{\mathrm dt}} = \cos{t}[/math].[math]\begin{align} \therefore T &= -e^{-tu}\cos{t} - u\int v\, \frac{\mathrm dw}{\mathrm dt} \,\mathrm dt \\ &= -e^{-tu}\cos{t} - uvw + u\int w\, \frac{\mathrm dv}{\mathrm dt} \,\mathrm dt \\ &= -e^{-tu}\cos{t} - ue^{-tu}\sin{t} + u\int -ue^{-tu}\sin{t} \,\mathrm dt \\ &= -e^{-tu}\left( \cos{t} + u\sin{t} \right) - u^2 T \end{align}[/math][math]\therefore \left( u^2 + 1 \right) T = -e^{-tu}\left( \cos{t} + u\sin{t} \right)[/math][math]\therefore T = \dfrac{-e^{-tu}\left( \cos{t} + u\sin{t} \right)}{u^2 + 1}[/math][math]\begin{align} \therefore \lim_{x \to \infty} \int_0^x e^{-tu}\sin{t} \,\mathrm dt &= \lim_{x \to \infty} \bigg[ \frac{-e^{-tu}\left( \cos{t} + u\sin{t} \right)}{u^2 + 1} \bigg]_0^x \\ &= \lim_{x \to \infty} \frac{1}{u^2 + 1} \left( -e^{-xu}\left( \cos{x} + u\sin{x} \right) - -e^0\left( \cos{0} - u\sin{0} \right) \right) \\ &= \frac{1}{u^2 + 1} \lim_{x \to \infty} \left( -e^{-xu}\left( \cos{x} + u\sin{x} \right) + 1 \right) \\ &= \frac{1}{u^2 + 1}\ \text{ QED} \end{align}[/math]Addendum Some further discussion of this integral and methods of solving it can also be found here: Evaluating the integral $\int_{0}^{\infty} \frac{\sin{x}}{x} \ dx = \frac{\pi}{2}$?
-
How do I integrate Chef Linux to VMware virtual box?
Your question is not clear. Could you let me know exactly what you want.Do you want to install chef server/workstation in linux VM ruuning in virtual box.Do you want to automate virtual box task using existing chef server.
-
How is it signNow to intergrate ethics in marketing management?
In my view, Marketing and advertising are completely unproductive and useless industries, yet they are where much of our consumer money goes to.A good product sells itself, word of mouth will do that. If I want to buy new shoes, I look around a bit. Advertising is full of lies, I stopped ling ago listening to it.Let me begin with 'open markets'.Open markets, with few regulations, can be a good thing, freedom is a good thing.With one particular freedom though, it's not so easy. The freedom of large corporations to do pretty much do as they please, has been going rampant, out of control. In Switzerland, where I am from, we have learned from a long history of free market, that the bigger a company grows, the more prone it becomes to neglecting social responsibilities and pro consumer policies. (Swiss examples: Nestlé, Glencore, Novartis) I believe this is partially due to the fact that the closeness to the consumer goes amiss. We can not expect politics to react anytime soon, for obvious economic considerations.A corporation's foremost goal is trade, profit, not consumer health or welfare. I am not complaining about that, it is logical, we have to expect it. What is NOT logical, is that we blindly buy what they advertise. We have a choice, it is called, 'Consumer choice'. If we neglect that liberty, we surrender our democratic rights to the corporate giants, their policies and their objectives, and we lose the right to complain.Instead of waiting for our politicians to take our side, we should begin to teach children/adolescents from elementary level on, about what a healthy and tasty 'diet' consists of, how different food products are made, by whom and with what ingredients, and whether some of them may adversely affect our health. We should let them in on basic deceiving marketing tactics that they will be faced with out on the street in everyday life. We should show them how to shape an informed opinion on issues that matter, and how to check facts by most importantly using common sense. Primarily, we should teach our children how to spot issues that matter versus those which don't.Alongside with changing what you consume at home, we should 'pressure' school principals into pressuring their school boards, into pressuring legislators to write legislation that would support building a better, more sustainable, more conscious and healthier world for the generations of human beings that will succeed us.The subject of advertising to minors, especially the more susceptible children under 12 years of age, is an issue we should deal with. Every parent can begin this process at home today, it's easy and fun. Children literally eat up new information, it is my humble opinion that we should give them useful knowledge and advice, instead of actual and intellectual 'junk food'.Any parent's first priority, or how we pay food corporations big money for making us sick
Trusted esignature solution— what our customers are saying
Get legally-binding signatures now!
Related searches to How To Integrate eSign in Box
Frequently asked questions
How do i add an electronic signature to a word document?
How do you know an electronic signature is real?
How to sign a pdf without certificate?
Get more for How To Integrate eSign in Box
Find out other How To Integrate eSign in Box
- Wisconsin application for absentee ballot form
- Nhs pensions deferred benefits claim form aw8pbe
- Wisconsin application for absentee ballot confidential elector id svrs id hindi sequential office use only office use only form
- Read the terms in section 8 and complete section 9 before returning your application form
- Florida supreme court approved family law form 12 995c relocationlong distance parenting plan 0218
- Securian beneficiary designation form
- Health certificate clearance application form
- Positive pay system key features bank of baroda form
- Madhya bihar gramin bank head office form
- Mitgliedschaftsantrag studenten tk form
- Visa application for morocco form
- Hoa 788 professional paper pre authorization registration form
- W 8ben e form
- Month to month lease agreement 695027915 form
- Early enforcement payment by centrepay instalments form
- Archivio cartelle cliniche gemelli telefono form
- Correction application form
- Tus digital badge earner application and consent form
- Debeka formulare zum ausdrucken
- Novo nordisk patient assistance program form