Test eSign with airSlate SignNow
Award-winning eSignature solution
Get the robust eSignature features you need from the solution you trust
Select the pro platform made for pros
Configure eSignature API quickly
Work better together
Test esign, in minutes
Cut the closing time
Maintain important data safe
See airSlate SignNow eSignatures in action
airSlate SignNow solutions for better efficiency
Our user reviews speak for themselves
Why choose airSlate SignNow
-
Free 7-day trial. Choose the plan you need and try it risk-free.
-
Honest pricing for full-featured plans. airSlate SignNow offers subscription plans with no overages or hidden fees at renewal.
-
Enterprise-grade security. airSlate SignNow helps you comply with global security standards.
Your step-by-step guide — test e sign
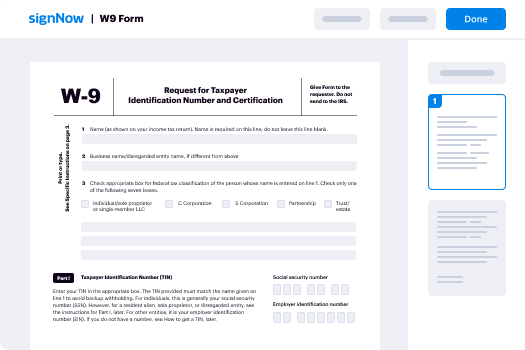
Using airSlate SignNow’s electronic signature any organization can speed up signature workflows and eSign in real-time, giving a better experience to customers and workers. test esign in a couple of easy steps. Our mobile-first apps make work on the go achievable, even while off the internet! eSign signNows from any place worldwide and close deals faster.
How to fill out and sign a test esign
- Sign in to your airSlate SignNow profile.
- Find your needed form in your folders or upload a new one.
- Open the document and make edits using the Tools menu.
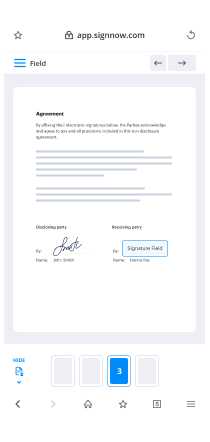
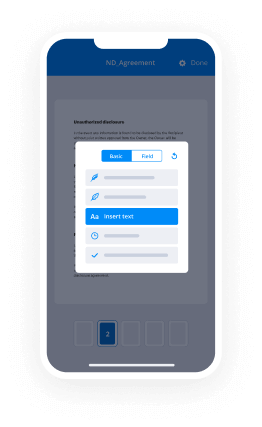
- Place fillable fields, add textual content and sign it.
- List multiple signees using their emails and set the signing order.
- Indicate which recipients will receive an executed version.
- Use Advanced Options to reduce access to the template and set an expiry date.
- Tap Save and Close when done.
Furthermore, there are more enhanced functions open to test esign. Add users to your common workspace, view teams, and keep track of collaboration. Millions of consumers across the US and Europe recognize that a system that brings people together in one cohesive workspace, is what companies need to keep workflows functioning efficiently. The airSlate SignNow REST API enables you to integrate eSignatures into your application, website, CRM or cloud storage. Try out airSlate SignNow and get quicker, smoother and overall more productive eSignature workflows!
How it works
airSlate SignNow features that users love
See exceptional results test esign
How to fill out and eSign a PDF online
Try out the fastest way to test e sign. Avoid paper-based workflows and manage documents right from airSlate SignNow. Complete and share your forms from the office or seamlessly work on-the-go. No installation or additional software required. All features are available online, just go to signnow.com and create your own eSignature flow.
A brief guide on how to test e sign in minutes
- Create an airSlate SignNow account (if you haven’t registered yet) or log in using your Google or Facebook.
- Click Upload and select one of your documents.
- Use the My Signature tool to create your unique signature.
- Turn the document into a dynamic PDF with fillable fields.
- Fill out your new form and click Done.
Once finished, send an invite to sign to multiple recipients. Get an enforceable contract in minutes using any device. Explore more features for making professional PDFs; add fillable fields test e sign and collaborate in teams. The eSignature solution supplies a reliable process and works according to SOC 2 Type II Certification. Be sure that your data are guarded and that no one can change them.
How to eSign a PDF in Google Chrome
Are you looking for a solution to test e sign directly from Chrome? The airSlate SignNow extension for Google is here to help. Find a document and right from your browser easily open it in the editor. Add fillable fields for text and signature. Sign the PDF and share it safely according to GDPR, SOC 2 Type II Certification and more.
Using this brief how-to guide below, expand your eSignature workflow into Google and test e sign:
- Go to the Chrome web store and find the airSlate SignNow extension.
- Click Add to Chrome.
- Log in to your account or register a new one.
- Upload a document and click Open in airSlate SignNow.
- Modify the document.
- Sign the PDF using the My Signature tool.
- Click Done to save your edits.
- Invite other participants to sign by clicking Invite to Sign and selecting their emails/names.
Create a signature that’s built in to your workflow to test e sign and get PDFs eSigned in minutes. Say goodbye to the piles of papers sitting on your workplace and begin saving time and money for extra essential duties. Picking out the airSlate SignNow Google extension is a great convenient decision with a lot of benefits.
How to eSign an attachment in Gmail
If you’re like most, you’re used to downloading the attachments you get, printing them out and then signing them, right? Well, we have good news for you. Signing documents in your inbox just got a lot easier. The airSlate SignNow add-on for Gmail allows you to test e sign without leaving your mailbox. Do everything you need; add fillable fields and send signing requests in clicks.
How to test e sign in Gmail:
- Find airSlate SignNow for Gmail in the G Suite Marketplace and click Install.
- Log in to your airSlate SignNow account or create a new one.
- Open up your email with the PDF you need to sign.
- Click Upload to save the document to your airSlate SignNow account.
- Click Open document to open the editor.
- Sign the PDF using My Signature.
- Send a signing request to the other participants with the Send to Sign button.
- Enter their email and press OK.
As a result, the other participants will receive notifications telling them to sign the document. No need to download the PDF file over and over again, just test e sign in clicks. This add-one is suitable for those who like focusing on more valuable tasks instead of burning up time for nothing. Enhance your day-to-day monotonous tasks with the award-winning eSignature platform.
How to eSign a PDF on the go without an app
For many products, getting deals done on the go means installing an app on your phone. We’re happy to say at airSlate SignNow we’ve made singing on the go faster and easier by eliminating the need for a mobile app. To eSign, open your browser (any mobile browser) and get direct access to airSlate SignNow and all its powerful eSignature tools. Edit docs, test e sign and more. No installation or additional software required. Close your deal from anywhere.
Take a look at our step-by-step instructions that teach you how to test e sign.
- Open your browser and go to signnow.com.
- Log in or register a new account.
- Upload or open the document you want to edit.
- Add fillable fields for text, signature and date.
- Draw, type or upload your signature.
- Click Save and Close.
- Click Invite to Sign and enter a recipient’s email if you need others to sign the PDF.
Working on mobile is no different than on a desktop: create a reusable template, test e sign and manage the flow as you would normally. In a couple of clicks, get an enforceable contract that you can download to your device and send to others. Yet, if you want an application, download the airSlate SignNow mobile app. It’s secure, quick and has an excellent design. Take advantage of in smooth eSignature workflows from your office, in a taxi or on a plane.
How to sign a PDF utilizing an iPhone
iOS is a very popular operating system packed with native tools. It allows you to sign and edit PDFs using Preview without any additional software. However, as great as Apple’s solution is, it doesn't provide any automation. Enhance your iPhone’s capabilities by taking advantage of the airSlate SignNow app. Utilize your iPhone or iPad to test e sign and more. Introduce eSignature automation to your mobile workflow.
Signing on an iPhone has never been easier:
- Find the airSlate SignNow app in the AppStore and install it.
- Create a new account or log in with your Facebook or Google.
- Click Plus and upload the PDF file you want to sign.
- Tap on the document where you want to insert your signature.
- Explore other features: add fillable fields or test e sign.
- Use the Save button to apply the changes.
- Share your documents via email or a singing link.
Make a professional PDFs right from your airSlate SignNow app. Get the most out of your time and work from anywhere; at home, in the office, on a bus or plane, and even at the beach. Manage an entire record workflow easily: make reusable templates, test e sign and work on PDFs with business partners. Transform your device right into a powerful company tool for closing deals.
How to sign a PDF using an Android
For Android users to manage documents from their phone, they have to install additional software. The Play Market is vast and plump with options, so finding a good application isn’t too hard if you have time to browse through hundreds of apps. To save time and prevent frustration, we suggest airSlate SignNow for Android. Store and edit documents, create signing roles, and even test e sign.
The 9 simple steps to optimizing your mobile workflow:
- Open the app.
- Log in using your Facebook or Google accounts or register if you haven’t authorized already.
- Click on + to add a new document using your camera, internal or cloud storages.
- Tap anywhere on your PDF and insert your eSignature.
- Click OK to confirm and sign.
- Try more editing features; add images, test e sign, create a reusable template, etc.
- Click Save to apply changes once you finish.
- Download the PDF or share it via email.
- Use the Invite to sign function if you want to set & send a signing order to recipients.
Turn the mundane and routine into easy and smooth with the airSlate SignNow app for Android. Sign and send documents for signature from any place you’re connected to the internet. Build good-looking PDFs and test e sign with just a few clicks. Put together a flawless eSignature process with only your smartphone and boost your overall productivity.
Get legally-binding signatures now!
FAQs test e sign
-
How do I comply with the eSign act?
Step 1 - Availability of airSlate SignNow Delivery or airSlate SignNow Copies. ... Step 2 - Consent Choices. ... Step 3 - Consumer Actions. ... Step 4 - Hardware/Software Requirements. ... Step 5 - Affirmatively Consent. ... Step 6 - "After Consent" Disclosure. -
How do I identify an electronic signature?
Open the file that contains the digital signature you want to view. Click File > Info > View Signatures. In the list, on a signature name, click the down-arrow, and then click Signature Details. -
What is an acceptable electronic signature?
Simply put, yes, digital signatures are valid and enforceable. As long as certain requirements are met, they have the same legal effect as their written equivalents. Like a traditionally signed contract, one of the most important elements of validity is the signing party's intent to be bound. -
What does e signature look like?
As for what your electronic signature will look like, it's up to you! Most electronic signatures look identical to pen and airSlate SignNow signatures. When creating your electronic signature with airSlate SignNow, you have the option to: ... Write your signature on a touchscreen using your finger or a stylus. -
What does Esign stand for?
Related to ESIGN: Electronic signature. Acronym. Definition. ESIGN. Electronic Signatures in Global and National Commerce Act. -
Is digital signature a part of electronic signature?
Digital Signatures. A digital signature is a type of electronic signature that offers more security than a traditional electronic signature. When you sign a document with a digital signature, the signature links a \u201cfingerprint\u201d of the document to your identity. -
Is a typed signature legally binding?
Does typed signature count? No. There are a number of eSignature laws across the world, such as ESIGN and UETA, which define what constitute a legally binding esignature. ... Simply typing your name into a document cannot tie the signature to the document. -
What program allows you to sign documents?
airSlate SignNow is an electronic signature app created by Citrix. Like most eSignature apps, airSlate SignNow allows you to upload, prepare, and send documents for signature\u2014as well as receive them, sign them, and return them to another sender. -
Is there an app where you can sign documents?
airSlate SignNow's mobile app for Android empowers you to sign documents and get signatures from anyone, anywhere. You can sign any document free, directly from your device. -
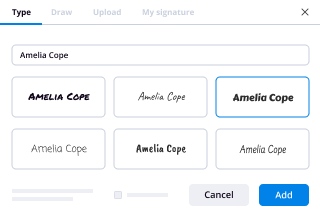
How do I do an electronic signature?
Draw your signature using your finger or a stylus. If you have access to a touchscreen, you can use your finger to create an electronic signature directly in your document. ... Upload an image of your signature. ... Use your cursor to draw your signature. ... Use your keyboard to type in your signature. -
How do I do an electronic signature on my phone?
Suggested clip Signing a Document on Android - YouTubeYouTubeStart of suggested clipEnd of suggested clip Signing a Document on Android - YouTube -
How do I get documents signed online?
Sign up for a free trial at airSlate SignNow, and then log in. Select New > Sign a Document, and then upload the electronic document. Select Sign and then follow the steps to electronically sign your document. -
How do I make an electronic signature on my Iphone?
Preview the attachment in the Mail app. Tap the toolbox icon, and then tap the Signature button in the Markup preview. Sign the document using your finger on the touchscreen, and then tap Done. Place the signature where it belongs in the document, and then tap Done again.
What active users are saying — test e sign
Frequently asked questions
What is the definition of an electronic signature according to the ESIGN Act?
How do I get a PDF ready for others to electronically sign it?
How do I sign and scan a PDF?
Get more for test esign
- Print electronic signature initials
- Print signature date
- Print sign date
- Print sign name
- Print signatory title
- Print signature block signature
- Fax electronically sign phone
- Forward electronic signature email
- Forward signature formula
- Forward sign email
- Forward email signature email
- Notarize mark phone
- Merge electronically sign payment
- Merge autograph formula
- Copy signature image
- Copy signature email
- Copy sign image
- Copy initials cc number
- Copy signed signature
- Copy signed zip
- Copy electronically sign formula
- Copy autograph signature
- Copy signed electronically formula
- Copy signed electronically number
- Copy electronically signing radio button
- Copy electronically signed gender
- Upload signature image
- Upload sign image