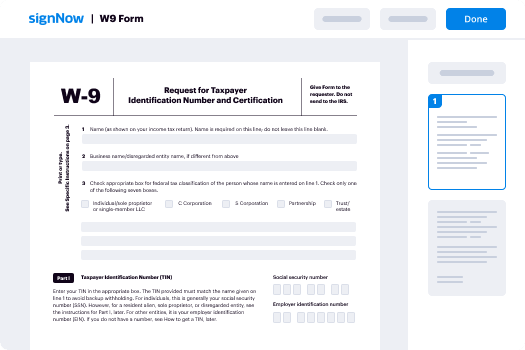
Use Kiosk Mode, Add Text Tags and eSign

I have been into writing from last couple of years. I tried creating a blog of my own, using right keywords and meta tags also, but didn’t see a lot of traffic coming in, except for a few friends and family (since I am not into digital marketing and all).Then I thought, why not try already available writing platforms. I tried a few I am giving you the list along with my experience of using them.PoemHunter.com : The website is an awesome place for sharing your work. There are lots of new-age writer. They also give you feedback. Although, through the interactions with other members, I felt th...

The Pauli Exclusion principle can be derived rather simply by considering a two particle state, so I’ll do it here, and hopefully that will answer your question.We consider a system comprised of two electrons, denoted 1 and 2, and we package their states into a state like so: [math]| 1,2 \rangle[/math].If electron 1 is in a state [math]\phi[/math], and electron 2 is in a state [math]\psi[/math], we can write this as:[math]\displaystyle |1,2 \rangle = |\phi(x_1) \rangle |\psi(x_2) \rangle \tag*{}[/math]For example.We now consider an operator called the “particle exchange operator”, [math]\hat{P}[/math].Quite simply, this operator swaps the two particles around — electron two now occupies electron 1’s original state, and vice versa.[math]\displaystyle \hat{P} |1,2\rangle = |2,1\rangle \tag*{}[/math]The trick is to note that electrons are identical. Therefore our system should not behave any differently if electrons are switched. The dynamics of a quantum system are determined by the absolute magnitude [math]\langle \psi |\psi \rangle[/math], so the only thing that [math]P[/math] can do is add a complex phase shift (since phase shifts automatically cancel in the magnitude operation, and hence adding a shift does not affect the dynamics).[math]\displaystyle \hat{P} |1,2 \rangle = |2,1 \rangle = e^{i \theta} |1,2 \rangle \tag*{}[/math]We can work out exactly what [math]\theta[/math] is by applying [math]\hat{P}[/math] to the [math]|2,1\rangle[/math] state:[math]\displaystyle \hat{P} |2,1 \rangle = |1,2 \rangle = \hat{P}^2 |1,2\rangle\tag*{}[/math]But we know that all [math]\hat{P}[/math] does is add a complex phase [math]e^{i \theta}.[/math]Therefore, [math]\hat{P}^2 |1,2\rangle = e^{2 i \theta} |1,2 \rangle = |1,2\rangle[/math]Therefore:[math]\displaystyle e^{2 i \theta} = 1 \quad \rightarrow \quad e^{i \theta} = \pm 1 \tag*{}[/math]That was a bit of a deluge of mathematics, so I will quickly summarise what I’ve shown so far:If you swap two identical particles around in a quantum system, you either leave the wavefunction unchanged, or you add a minus sign.Both of these systems (as expected) produce the same dynamics when squared, as the minus sign cancels out.We call the particles which use +1 under particle exchange bosons, and particles which have -1 fermions.In other words:[math]\displaystyle \hat{P} |1,2\rangle = \begin{cases} |1,2\rangle & \text{for bosons} \\ -|1,2\rangle &\text{for fermions} \end{cases} \tag*{}[/math]You may have heard the definition that fermions have half-integer spin and bosons have integer spin. This is an equivalent definition, but is a) much more complex (requires the relativistic spin-statistics theorem) and b) historically came after this definition.OK. What does this have to do with Pauli Exclusion principle?Well, the problem is is that this exchange sign limits what states we can construct.Let’s try to write out explicitly a state for [math]|1,2\rangle[/math]Let’s use our original expansion in terms of [math]\psi[/math] and [math]\phi[/math]:[math]\displaystyle |1,2 \rangle = |\phi(x_1) \rangle |\psi(x_2) \rangle \tag*{}[/math]Now — let’s use [math]\hat{P}[/math] on this system.[math]\displaystyle \hat{P}|1,2 \rangle = |\phi(x_2) \rangle |\psi(x_1) \rangle \tag*{}[/math]But….We require that for a boson, [math]\hat{P} |1,2 \rangle = |1,2\rangle[/math]But…that is only true if [math]\phi = \psi[/math]! That’s not true in general….And for a fermion, we need a minus sign, which we don’t have any which way we look at it.What is going on?The requirements that particles are identical is limiting how we can construct our quantum systems!We need to think of a new way of writing them down.As a random guess — let’s try writing a system as:[math]\displaystyle |1,2\rangle = \left( |\phi(x_1), \psi(x_2)\rangle + |\psi(x_1), \phi(x_2) \rangle \right) \tag*{}[/math]If we use our exchange operator on this, then we get:[math]\displaystyle \hat{P}|1,2\rangle = \left( |\phi(x_2), \psi(x_1)\rangle + |\psi(x_2), \phi(x_1) \rangle \right) \tag*{}[/math]Which is…just [math]|1,2\rangle[/math] with the two addition terms switched around!We have found a way to write a boson’s quantum state which obeys the exchange symmetry!If we try this with a minus sign, we find that:[math]\displaystyle \hat{P} \left( |\phi(x_1), \psi(x_2)\rangle - |\psi(x_1), \phi(x_2) \rangle \right) = \left( |\phi(x_2), \psi(x_1)\rangle - |\psi(x_2), \phi(x_1) \rangle\right) \tag*{}[/math]This is just minus the original state — this is a valid way to write a fermions state in a two particle system!OK, we can now summarise:For a system of two particles, in states [math]\psi[/math] and [math]\phi[/math] respectively, the only ways to write them which obeys exchange symmetry is as follows:[math]\displaystyle |1,2\rangle = \begin{cases} |\phi(x_1),\phi(x_2)\rangle &\text{if boson, and } \phi = \psi \\ \frac{1}{\sqrt{2}} \left(|\phi(x_1),\psi(x_2) \rangle + |\phi(x_2),\psi(x_1) \rangle \right) & \text{if boson and} \phi \neq \psi \\ \frac{1}{\sqrt{2}} \left(|\phi(x_1),\psi(x_2) \rangle - |\phi(x_2),\psi(x_1) \rangle \right) & \text{if fermion} \end{cases} \tag*{}[/math]Phew. The extra factors of [math]\frac{1}{\sqrt{2}}[/math] are just normalisation factors, so that [math]\langle 1,2|1,2\rangle = 1[/math].It’s not entirely obvious yet, but we’ve actually just proved the Pauli Exclusion principle.Let’s first consider a boson, with two particles initially in different states [math]\psi[/math] and [math]\phi[/math]. We then introduce some potential which pushes them into the same state.What happens? Well…nothing.We can perfectly well describe a bosonic state by [math]|1,2\rangle = |\phi(x_1),\phi(x_2)\rangle[/math]All’s well there — two bosons can occupy the same quantum state.But if we try this same trick with a fermionic state?Well, our state is:[math]\displaystyle |1,2\rangle = \frac{1}{\sqrt{2}} \left(|\phi(x_1),\psi(x_2) \rangle - |\phi(x_2),\psi(x_1) \rangle \right) \tag*{}[/math]If we then let [math]\phi \to \psi[/math] …[math]\displaystyle |1,2\rangle = \frac{1}{\sqrt{2}} \left(|\phi(x_1),\phi(x_2) \rangle - |\phi(x_2),\phi(x_1) \rangle \right) \tag*{}[/math]And when we force them into the exact same state — [math]x_1 = x_2[/math], we find….[math]\displaystyle |1,2\rangle = 0 \tag*{}[/math]Ah.That is problematic.Our quantum state vanished.That means there is zero probability of finding two identical fermions in the same quantum state.And that is the Pauli Exclusion Principle!The Pauli Exclusion Principle arises from:Identical particlesWhich have a sign change under particle exchangeAnd then simply calculating how this requirement affects what quantum states we can write.This means that, by definition, bosons are not affected by it — because bosons are defined as not having a sign change under particle exchange.Since they do not have this sign-change-requirement, bosons are not restricted in this way, and can happily occupy the same quantum state.Fermions on the other hand, simply due to the mathematics of particle exchange, are restricted.It’s a seemingly very odd result that just thinking about what happens when you swap two particles around fundamentally limits what you can do with those two particles.But if you follow the mathematics through carefully, it is entirely logical that this result follows.Weird, right?

Tools such as airSlate SignNow(website) and signNowSign(website) are gaining popularity for businesses because they provide quality solutions for electronic signature. In particular advantages such as these take them to a new level:Get documents eSigned anytime, anywhere, on any device while keeping the spotlight on your brandSecure your documents and each person's signature using military-grade, digital signature technologyProve your compliance and deflect legal disputes with the most comprehensive audit trails

Yes! And I bet I can do it in a way that most of you have never seen before. Also, most of the other answers here require that you know[math]\displaystyle{\int_{0}^{\infty} e^{-x^2} dx = \dfrac{\sqrt{\pi}}{2}}[/math]But the only requirement you need to know for this answer is[math]e^{ix} = \cos{x}+i\sin{x}[/math]Which I don't consider to be ‘complex analysis' in the slightest.(Oh, and you also need to know some integration and differentiation techniques, but nothing too complicated.)Now for the moment of truth…We introduce the (extraordinary!) function[math]\displaystyle{G(x)=\left\{\int_{0}^{x}e^{it^2}dt\right\}^2+i\int_{0}^{1}\dfrac{e^{ix^2(t^2+1)}}{t^2+1}dt}[/math]Now let's differentiate [math]G(x)[/math]. We have two integrals, and we differentiate them in different ways. The first is much easier since[math]\displaystyle{\dfrac{d}{dx}\int_{0}^{x}e^{it^2}=e^{ix^2}}[/math]And then we use the chain rule bec...

How do I integrate: exp(-x²) sin(x²) , with x from 0 to infinity? In my modest advertising campaign to think and work generically I would go as far as paraphrasing the saying by Albert Einstein make it as simple as possible but not simpler intomake it as generic as possible but not too genericAs such, consider two, as is often fruitful, integrals as functions in two real variables [math]a[/math] and [math]b[/math] such that [math]a>0, b\geqslant 0[/math]:[math]\displaystyle C(a,b)=\int_0^{+\infty}e^{-ax^2}\cos bx^2\;dx \tag{1}[/math][math]\displaystyle S(a,b)=\int_0^{+\infty}e^{-ax^2}\sin bx^2\;dx \tag{2}[/math]which constitute a happy marriage of two, famous by now, integrals - that of Fresnel:[math]\displaystyle \int_0^{+\infty}\cos x^2\;dx=\int_0^{+\infty}\sin x^2\;dx = \dfrac{\sqrt{2\pi}}{4} \tag*{}[/math]and that of Euler-Poisson:[math]\displaystyle \int_0^{+\infty}e^{-x^2}\;dx = \dfrac{\sqrt{\pi}}{2} \tag*{}[/math](which we compute in this Quora answer).Take the first partial derivatives of [math]C(a,b)[/math] and [math]S(a,b)[/math] with respect to [math]b[/math] using the rule due to G. Leibniz:[math]\displaystyle \dfrac{\partial C(a,b)}{\partial b}=-\int_0^{+\infty}x^2e^{-ax^2}\sin bx^2\;dx \tag{3}[/math][math]\displaystyle \dfrac{\partial S(a,b)}{\partial b}=\int_0^{+\infty}x^2e^{-ax^2}\cos bx^2\;dx \tag{4}[/math]Integrating the R...

1. Knowing who is your Audience2. Relevant Content3. Keyword relevant Url structure  4. Keyword Relevant Titles5. Have keyword anchor text density below 5%6. Back-link from sites with high DA,PA,Trust,Citation,PR7. Adding Youtube videos on site8. STAY AWAY FROM LINK FARMS9. Utilizing LSI keywords  10. Doing PPC lol

On the one hand, when we integrate [math]x, x^2, x^3, x^4[/math] and so on we get a nice, predictable pattern and on the other hand, when we integrate [math]x^{-2}, x^{-3}, x^{-4}[/math] and so on we also get a nice, predictable pattern.However, when we try to integrate [math]x^{-1}[/math] then we get … a hiccup in the pattern.What is going on here?It is understandable that even when people are told what the answer is they, nonetheless, walk away confused. My answer to this type of confusions - put on the boots and walk to the top - yourself, every inch of the way.Between the above two families of integrals there lies a discovery - of a new function by the Scott John Napi...

From your question I inferred you are talking about online/web-based applications. Obviously there are other applications, like standalone medical devices, etc. that have a different story. Assuming that, let's divide the problem into four components:1- You need a database. Your choice depends on different aspects but most important thing is size and speed of your data. For small sized problems a regular RDBMS will do the job.2- You need a component to build dynamic HTML pages. A typical web programming language like PHP will do that job. Your dynamics HTML component manages communication w...